Erwartungswert und Standardabweichung (a)

(Oft werden die möglichen Werte statt mit a_i auch mit x_i bezeichnet.)

Man kann zeigen, dass für den Erwartungswert der Zufallsgröße X: Anzahl der Erfolge bei einem n-stufigen Bernoulli-Versuch gilt:

m = E(X) = n · p.

Der Erwartungswert gibt uns eine "Punktschätzung" über ein zu erwartendes Zufallsergebnis. Die "Breite" einer Verteilung wird durch andere Kenngrößen beschrieben ...

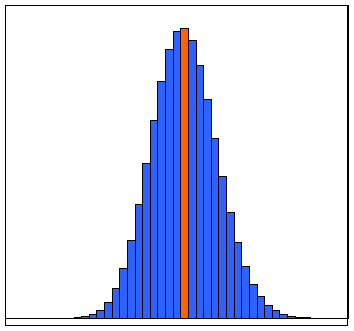
Das Maximum einer Binomialverteilung liegt stets in der Nähe des Erwartungswertes. Genauer gesagt: die Erfolgsanzahl k, für die P(X=k) maximal ist, hat den minimalen Abstand zu m (das ja nicht notwendig eine natürliche Zahl ist).