b) Wie groß ist die Wahrscheinlichkeit, dass man (i) weniger als 14, (ii) mehr als 14 (iii) 7 bis 21 Rückfällige findet?

Mit n=70 und p=20% lautet die Binomialverteilung

(i) Gesucht ist P(X<14). Dafür müssen die Werte P(X=k) für k=0 bis k=13 summiert werden. Es ergibt sich eine Wahrscheinlichkeit von etwa 45,2%. 

(ii) Gesucht ist P(X>14). Zur Reduktion des Rechenaufwands bestimmt man am besten die Gegenwahrscheinlichkeit P(X£15)»57,1% und subtrahiert diese von 100%. Es ergibt sich eine Wahrscheinlichkeit von  P(X>14)»42,9%.

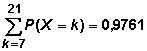
Mit der Wahrscheinlichkeit von 97,6% wird man also bei einer Untersuchung von 70 positiv begutachteten Sexualstraftätern 7 bis 21 Rückfällige finden. 

(Steht einem eine Tabelle mit der kumulierten Binomialverteilung zur Verfügung, so rechnet man hier P(X£21)-P(X£6).)