Drehkörper - Volumen- und Mantelflächenberechnungen |
Baustein 1 - 5(13) |
Rotationskörper in der Mathematik |
|
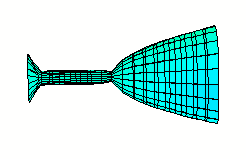
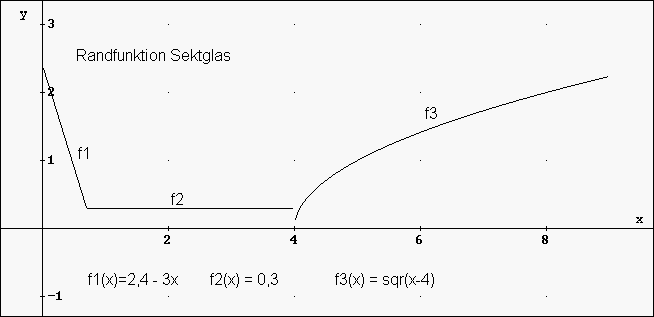
In der Mathematik untersucht man Rotationskörper, indem man die Außenlinie der rotierenden Fläche durch eine Funktion annähert. Das heißt, dass die Mathematiker eine (oder mehrere) Funktionen betrachten, deren Graph(en) diese Außenlinie repräsentieren. Als Rotationsachse wählt man hierbei meistens die x-Achse. Rotiert nun das Kurvenstück um die x-Achse, erzeugt es dabei den Mantel des Rotationskörpers.
Ausgehend von einer Problemstellung ...
... die Mathematisierung:
|
|
|
|
|