Drehkörper - Volumen- und Mantelflächenberechnungen |
Baustein 1 - 7(13) |
Bekannte Drehkörper - Kegel |
|
|
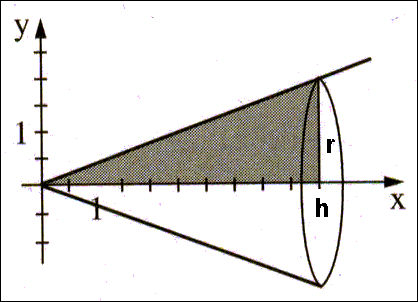
Ebenso kann man durch eine
Ursprungsgerade, die zum Beispiel um die x-Achse kreist, einen Kegel
erzeugen:
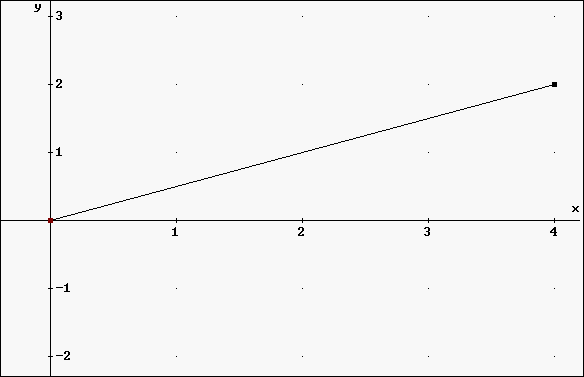
Dazu ein möglicher Graph im Derivefenster:
Aufgabe 3: a) Berechnen Sie mit den Ihnen aus der Mittelstufe bekannten Methoden das Volumen V eines Kegels mit dem Radius r = 5cm und Höhe h = 12cm. b) Wie lautet die Gleichung der Randfunktion, die in obiger Graphik (Derivefenster) bei Rotation um die x-Achse einen Kegel erzeugt? Was bedeutet das für den Radius r des Kegels? c) Welches Volumen V hat der zugehörige Kegel, dessen Höhe h von x = 0 bis x = 4 reicht? |
|
|
|
|