Drehkörper mit beliebiger stetiger Randfunktion
Im rheinischen Braunkohlerevier
sind die Kohlekraftwerke mit riesigen Kühltürmen versehen.

(Ansicht des Braunkohlekraftwerks Niederaußem / Rhein.
Braunkohlerevier / westlich von Köln)
Form, Höhe, Basisdurchmesser
am Boden und Mündungsradius an der Austrittsöffnung eines
Kühlturms haben wesentlichen Einfluss auf die Leistungsfähigkeit
eines Kraftwerks. Diese Vorgaben bestimmen das Volumen eines Kühlturms.

(Der 200m hohe Naturzug-Nasskühlturm des 950-MW-Braunkohlen-
blocks mit optimierter Anlagentechnik (kurz: BoA)
in Niederaußem westlich von Köln)
Bevor später im Lehrgang auch der obige 200m
hohe Kühlturm untersucht werden soll, sind einige Vorüberlegungen
notwendig.
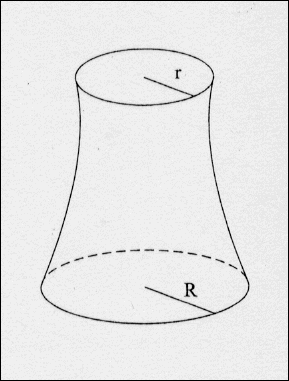
Ein Kühlturm (wie oben) ist näherungsweise ein Rotationskörper.
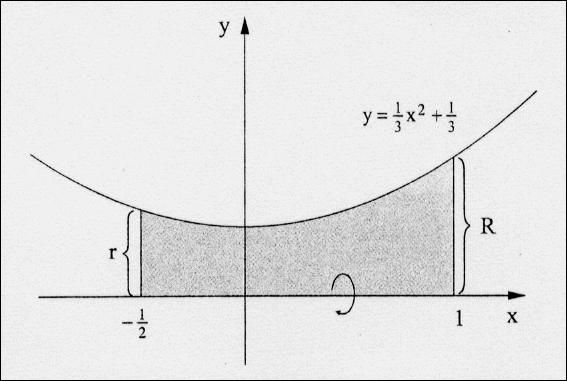
Man kann diesen Körper in Gedanken dadurch erzeugen, dass man
ein krummliniges Trapez um die x-Achse rotieren lässt. Im folgenden
Beispiel hat das krummlinige Trapez die Randfunktion f mit der Gleichung
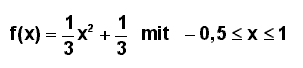
Hierbei soll eine Längeneinheit 100m in der
Realität entsprechen.
(Die Aufgabe entstammt der Aufgabensammlung
"Analysis Unterrichts-Materialien für Lehrkräfte
Sek II",
Stark-Verlag Freising)
Aufgabe 5:
a) Wie hoch ist der Kühlturm in diesem Beispiel?
b) Bestimmen Sie den Basisradius R und den Mündungsradius
r für diesen Kühlturm.
c) Bestimmen Sie den Taillenradius
rt (an der engsten Stelle) des Kühlturms.
In welcher Höhe befindet sich die Taille
des Kühlturms?
Es geht im Folgenden darum, rechnerisch das Volumen
dieses Beispiel-Kühlturms zu bestimmen. Hierbei helfen die
Methoden der Integralrechnung.
|





|
|