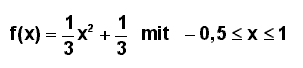Drehkörper - Volumen- und Mantelflächenberechnungen

Baustein 1 - 10(13)

Bevor das Volumen des Kühlturms aus Aufgabe 5 berechnet werden soll, sollen Sie sich mittels des untenstehenden Java-Applets von Felix Riedel die Rotation des zugehörigen Graphen um die x-Achse veranschaulichen. Die Randfunktion des Kühlturms

ist bereits voreingestellt.

Vor allem geht es bei diesem Applet darum, den Grundgedanken der Integralrechnung zur Volumenberechnung von Drehkörpern zu erfassen.

Veranschaulichen Sie sich die sogenannte "Scheibenmethode" mit diesem Applet,
indem Sie zwischen Unter- und Obersumme wechseln und Sie den Schieber oben mit der
Maus ziehen um dadurch die Anzahl der "Scheiben" zu erhöhen!

Wie im Applet zu sehen ist, liefert uns die Integralrechnung die Lösung des Problems. Analog zur Flächeninhaltsberechnung (für Flächen zwischen x-Achse und Funktionsgraph) teilen wir das Intervall [ - 0,5 ; 1 ] in beliebig viele Teilintervalle gleicher Breite ein. Wir erhalten so eine Vielzahl zylinderförmiger Scheiben, deren Volumina wir mit herkömmlichen Methoden berechnen können (siehe Baustein 1 - 6 ). Je kleiner wir die Breite dieser Teilintervalle wählen, umso besser nähert sich die Summe der einzelnen Scheibenvolumina an das tatsächliche Volumen des Kühlturms an.

Aufgabe 6:

Teilen Sie das Intervall [ - 0,5 ; 1 ] in

a) 3

b) 6

gleich große Teilintervalle und bestimmen Sie näherungsweise das Volumen des Kühlturms, indem Sie zunächst für jedes Teilintervall das Volumen der entsprechenden Zylinderscheibe bestimmen und dann die einzelnen Volumina aufsummieren. Wählen Sie hierbei als Zylinderradius stets den größten Funktionswert jeden Intervalls ("Obersumme").