Verallgemeinerung
der Scheibenmethode zur Volumensformel
In Aufgabe 6 näherten wir das Kühlturmvolumen an, indem
wir den Kühlturm in Zylinderscheiben gehüllt haben (Obersumme).
Hierbei entspricht die Höhe jeder Zylinderscheibe
der gewählten Intervallbreite Dx
. Der Radius r ergibt sich durch den größten Funktionswert
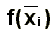 des
entsprechenden Intervalls.
1. Näherung des Kühlturmvolumens mit Dx
= 0,5 ergab: V » 1.243.500 m3
2. Näherung des Kühlturmvolumens mit Dx
= 0,25 ergab: V » 1.031.900 m3
Analog hierzu hätte man das Volumen annähern können,
indem man den Kühlturm mit Zylinderscheiben füllt (Untersumme).
Als Radius r ergibt sich hierbei der kleinste Funktionswert 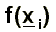 des
entsprechenden Intervalls.
Betrachten Sie dies nochmals am Applet: 
Je kleiner nun die Intervallbreite Dx
wird, desto genauer wird das tatsächliche Kühlturmvolumen
mit der Obersumme und der Untersumme angenähert. Im Applet
sehen Sie dies, wenn Sie den Schieber oben betätigen.
Betrachten Sie auch dies nochmals am Applet:
Integralnäherung:
Wenn Dx
nun gegen Null strebt, d.h. die Zylinderhöhen
unendlich klein werden, so strebt die Differenz zwischen Ober- und
Untersumme gegen Null: Die Summe der Zylindervolumina ergibt dann
das tatsächliche Kühlturmvolumen.
Um nun die
Volumenberechnungsformel der Integralrechnung zu erhalten, betrachten
wir den Übergang für Dx
gegen Null:
Ergebnis: Volumenformel für
Drehkörper
|
|
|
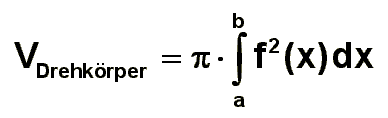
