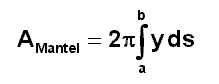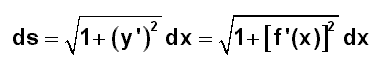Drehkörper - Volumen- und Mantelflächenberechnungen

Baustein 3 - 2(4)

Bestimmung des Mantelflächeninhalts von Rotationskörpern
(nur für Leistungskurse)

2. Die Berechnung der Mantelfläche bzw. der Oberfläche von Rotationskörpern

Wir betrachten eine Kurve als Graph einer Funktion f mit der Gleichung y=f(x) im Intervall [a ; b].

(Bildquelle: TCP 2001, CD zu: Mathematik Gymnasiale Oberstufe. PAETEC-Verlag )

Die Kurve (der Graph zu f ) rotiere nun um die x-Achse. Dabei überstreift die Kurve die Mantelfläche des entstehenden Drehkörpers.

Die Kurve im Intervall [a ; b] wird nun in einzelne Kurvenstücke der Länge ds zerlegt (siehe Abbildung oben).
Eines dieser Kurvenstücke überstreicht dann einen kleinen Teil des Mantels. Es entsteht so ein schmales, reifenförmiges Band.

Schneidet man das Band auf, so entsteht näherungsweise ein Rechteck mit den Seitenlängen ds und 2·p·y.

Daher gilt für den Flächeninhalt dA des schmalen Bands:   dA » 2py·ds

Hieraus ergibt sich (analog wie bei der Berechnung der Bogenlänge; vgl. oben) durch Integration als Mantelfläche des Rotationskörpers im Intervall [a ; b]:

Nun gilt für die Bogenlänge im Intervall [a ; b]:

Daraus ergibt sich:

Eingesetzt in A_Mantel ergibt sich damit die Berechnungsformel für die Mantelfläche eines Drehkörpers: