Drehkörper - Volumen- und Mantelflächenberechnungen

Baustein 3 - 1(4)

Bestimmung des Mantelflächeninhalts von Rotationskörpern
(nur für Leistungskurse)

1. Die Berechnung der Bogenlänge ebener Kurven

Um eine Berechnungsformel für die Mantelfläche bzw. den Mantelflächeninhalt eines Drehkörpers herzuleiten, ist zunächst die Berechnung der Bogenlänge ebener Kurven erforderlich.

Eine bekannte "ebene Kurve" ist der Kreis, dessen "Bogenlänge" sich als Kreisumfang U berechnen lässt:
U = 2·p·r (mit r = Radius des Kreises).

Ebenso lässt sich leicht die Länge eines Kreisbogens berechnen:
b=(a : 360°)·U .

Schwieriger ist nun die Berechnung der Länge ebener Kurven.

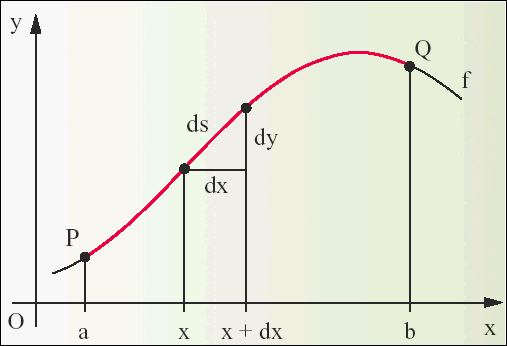
Dazu betrachten wir den Graphen (die "ebene Kurve") einer beliebigen (stetigen) Funktion f in einem
Intervall [a ; b] zwischen zwei Punkten P und Q:

(Bildquelle: TCP 2001, CD zu: Mathematik Gymnasiale Oberstufe. PAETEC-Verlag )

Dann gilt für die Bogenlänge s des Kurvenbogens zwischen den beiden Punkten P und Q (mit y=f(x)):

(zur Herleitung der Formel siehe   )
Auf die Anwendung der Formel auf konkrete Beispielaufgaben wird verzichtet, da der Schwerpunkt des Selbstlernmaterials auf der Berechnung von Volumina und Mantelflächen bei Rotationskörpern liegt.