Die Berechnung der Bogenlänge ebener Kurven

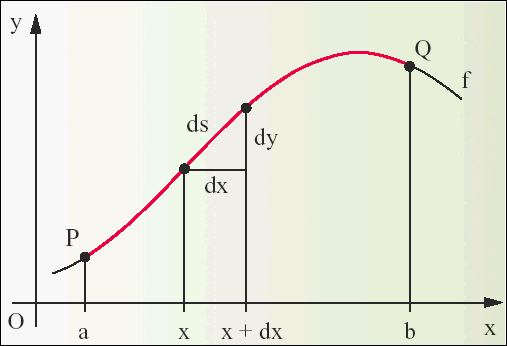
Zur Herleitung der Berechnungsformel betrachten wir den Graphen (die "ebene Kurve") einer beliebigen (stetigen) Funktion f in einem Intervall [a ; b] zwischen zwei Punkten P und Q:

(Bildquelle: TCP 2001, CD zu: Mathematik Gymnasiale Oberstufe. PAETEC-Verlag )

Man setzt zunächst y=f(x).

Für das Bogenstück ds gilt nach dem Satz des Pythagoras:    (ds)² » (dx)² + (dy)^{2
Daraus ergibt sich:}

^{Bildet man nun die Summe aller zwischen den Punkten P und Q liegenden Kurvenstücke ("Bogenstücke") und lässt ihre Anzahl durch immer feinere Unterteilung gegen ¥ gehen, so integriert man und man erhält für die Länge der Kurve:}

Auf die Anwendung der Formel auf konkrete Beispielaufgaben wird verzichtet, da der Schwerpunkt des Selbstlernmaterials auf der Berechnung von Volumina und Mantelflächen bei Rotationskörpern liegt.