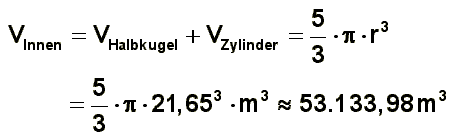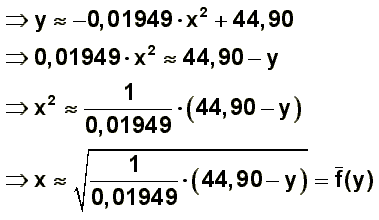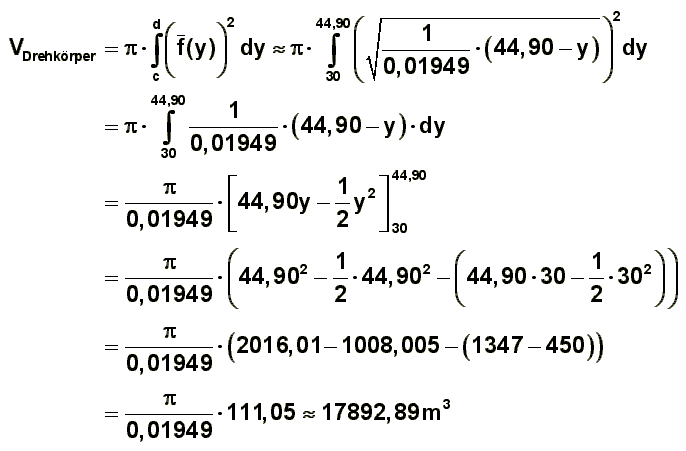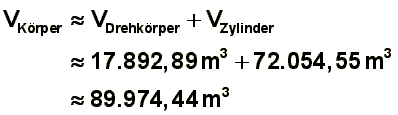Lösung zu Übungsaufgabe 13b:

Volumen des Baukörpers: Wie viel Kubikmeter römischer Beton wurde verbaut?

Berechnung des Rauminhalts für den Innenraum des Pantheons:

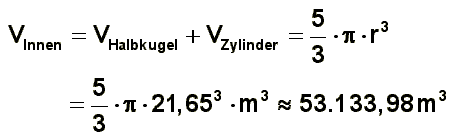
Berechnung des Volumens für die Kuppelöffnung:

          

Es wird angenommen. dass die Öffnung in der Kuppel zylinderförmig ist und einen Durchmesser von 9,00m sowie eine Höhe von h = 1,60m hat. Dann ergibt sich für das Volumen der Kuppelöffnung:

Das Volumen des Baukörpers berechnet sich aus dem Volumen des Körpers (Außenmaße) minus dem Volumen des Innenraums minus dem Volumen der Kuppelöffnung plus dem Volumen des Fundaments:

V_Baukörper = V_Körper - V_Innen - V_{Kuppelöffnung} + V_Fundament

Berechnung des Körpervolumens als Summe eines Drehkörpervolumens und eines Zylinders:

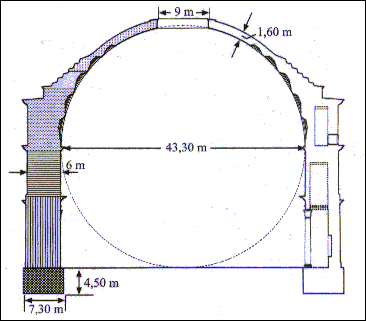
Die äußere Randkurve sei parabelförmig und symmetrisch zur y-Achse. Die Funktionsgleichung einer solchen Parabel lautet: f(x) = ax² + b . Um die Werte von a und b zu bestimmen, werden folgende Punkte P und Q aus der Querschnittsskizze des Pantheons (siehe oben) entnommen:

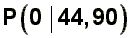
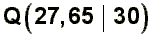
Damit lässt sich die Funktionsgleichung zu f bestimmen:

Die zugehörige Parabel rotiert nun um die y-Achse. Für die Berechnung des Drehkörpervolumens benötigt man die Umkehrfunktion zu f:

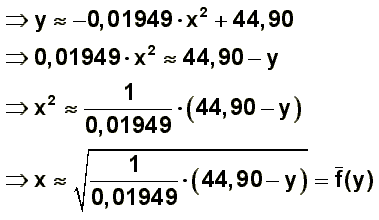
Daher ergibt sich für das Volumen des Drehkörpers:

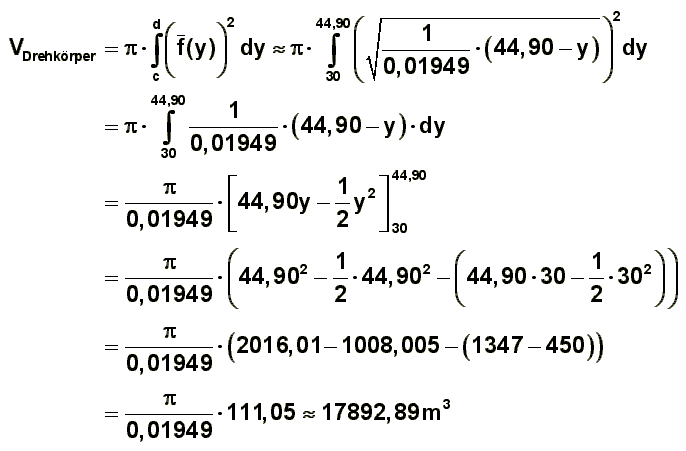
Berechnung des Volumens für den Zylinder (Außenmaße):



Damit ergibt sich für das Volumen des Körpers (mit den Außenmaßen des Pantheons):

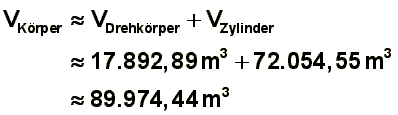
Berechnung des Volumens für das Fundament:



Damit erhält man nun das Volumen des Baukörpers:

Also wurden rund 42.000 m³ römischer Beton für das Pantheon verbaut. Diese Betonmenge würde einen Würfel mit ca. 34,75m Kantenlänge füllen.

Anmerkung: Bei der Berechnung der Betonmenge wurden Hohlräume im Baukörper, Abstufungen, Türen usw. nicht berücksichtigt. Daher wird die tatsächliche Betonmenge etwas kleiner sein.