Beurteilende Statistik - Baustein 2-1n

Stochastik - Beurteilende Statistik
2 Schluss von der Stichprobe auf die Gesamtheit

Baustein 2 - 1n

2-1 Sonntagsfrage

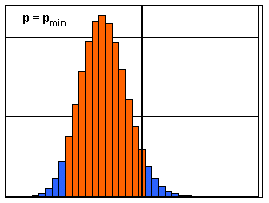
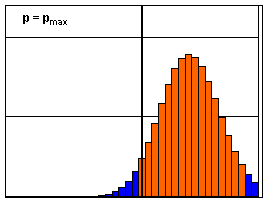
1. Schritt: Zu lösen sind die zwei Gleichungen

2. Schritt: Bestimmungsgleichung für p=p_min bzw. p=p_max:

1,96² ·n·p·(1-p) = (X-np)².

3. Schritt: Ausmultiplizieren ergibt (mit n=1000 und X=380):

1,96² ·1000p - 1,96² ·1000p² = 380²- 2·380·1000p + 1000²p²

Jetzt wird nach Potenzen von p sortiert und die quadratische Gleichung in Standardform gebracht:

1003841,6p²- 763841,6p + 144400 = 0 | :1003841,6

Also: p²- 0,760918455p + 0,143847395 = 0

Ah, pq-Formel! Das kenne ich!