Wahrscheinlichkeiten für eine Sigma-Umgebung (c)

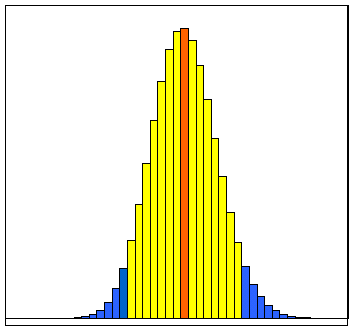
Da die Histogramme (für große n) nahezu symmetrisch zum Erwartungswert E(X)=m=n·p sind, betrachtet man symmetrische Bereiche um den Erwartungswert m. Man interessiert sich für z.B. für die symmetrische Umgebung von m, in der man ein Ergebnis mit einer Wahrscheinlichkeit von 90% findet. Man nennt diese Umgebung das 90%-Sicherheitsintervall.

Man könnte die Einzelwahrscheinlichkeiten P(X=k) so lange aufsummieren, bis man die gewünschte Sicherheitswahrscheinlichkeit erreicht hat. Das ist aufwändig! Es gibt aber eine Faustregel, die (bei Vorgabe von n, p und der Sicherheitswahrscheinlichkeit) den Radius des Intervalls liefert. Dabei bezeichnet man als Radius den Abstand der Intervallränder vom Erwartungswert.

Raus mit der Sprache!
Wie lautet diese Faustregel?