Drehkörper - Volumen- und Mantelflächenberechnungen

Baustein 1- 13(13)

(Unterschiedliche Abmessungen von Naturzugkühltürmen gleicher Kühlleistung)

Im Folgenden sollen weitere Kühlturmvolumina berechnet werden. Dazu muss allerdings zuerst ein sogenanntes "Steckbriefproblem" gelöst werden, um einen Funktionsterm für die Randfunktion zu erhalten. Im Allgemeinen ist die Randfunktion eine Hyperbel der Form 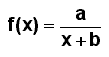. Da jedoch hier meist ein sehr komplexer Funktionsterm zu bestimmen ist, nähern wir die Randfunktion, deren Graph durch Rotation um die x-Achse den Drehkörper erzeugt, durch eine quadratische Funktion f an: f(x) = a·x² + b·x + c mit a, b, c Î IR.
Dies scheint zudem gerechtfertigt, da z. B. der Kühlturm A (s. o.) an seiner Mündung die engste Stelle aufweist.

Zu Kühlturm A: Für die gesuchte (Näherungs-)Randfunktion f gilt:

(1) f(0) = 148 / 2 = 74
(2) f(80) = 97 / 2 = 48.5
(3) f '(80)=0 (Die engste Stelle des Kühlturms soll ganz oben an der Mündung sein.)

Eine Lösung bestimmen wir nun z. B. mit DERIVE. Minimieren Sie das Fenster und klicken Sie auf den Button:

Definieren Sie im Algebrafenster die Funktion

f(x) := a·x² + b·x + c

Aus der Zeichnung ergeben sich folgende Bedingungen für die Bestimmung des Funktionsterms:

(1) f(0)=74 Û c = 74
(2) f(80)=48.5 Û a·6400 + b·80 + c =48.5
(3) f '(148)=0 Û 2·a·80 + b = 0

Entweder löst man nun das lineare Gleichungssystem mit dem Befehl LÖSEN > SYSTEM oder man benutzt den SOLVE-Befehl in DERIVE :

SOLVE([f(0)=74, f(80)=48.5, f '(80)= 0],[a,b,c])

Man erhält:  
  

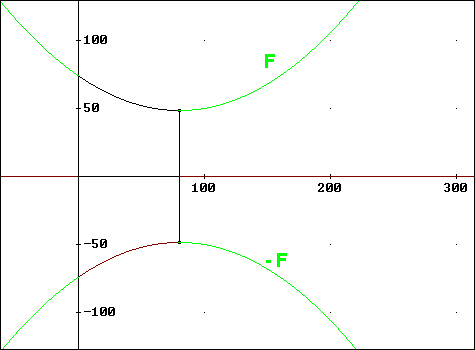
Man quadriert die Funktion F, integriert diese anschließend mit DERIVE und multipliziert das Ergebnis mit p.

Man erhält: V » 8,31·10⁵ m^{3
Vergleichen Sie hierzu den DERIVE-File kuehlturm-a.dfw !}

Aufgabe 7:

Bestimmen Sie analog eine quadratische Randfunktion und das Volumen für den Kühlturm B mit DERIVE. Auch bei Kühlturm B soll bei der Mündung die engste Stelle sein.